Class Name: Blend Directional Light

Superclass - <Directional Light Behaviour>

Subclasses

Definition

An instance of this DRM class specifies a <Directional Light Behaviour> instance, the intensity of which varies depending on the position of the observer relative to the light's location, direction, and shape. This light takes the shape of a pyramid, subdivided by two planes. These planes are based at the apex of the pyramid and extend towards the base. They subdivide the pyramid into upper, blend, and lower sections. If the observer is in the upper section, the primary colour is displayed. If the observer is in the lower section, the secondary colour is displayed. If the observer is in the blend section, the colour displayed is a proportional blend of the primary and secondary colours as defined below.

NOTE  The positive and negative ends of the SE_REFVEC_VERTICAL_AXIS vector correspond to upper and lower, respectively.

Primary Page in DRM Diagram:

• 21

Secondary Pages in DRM Diagram:

Example

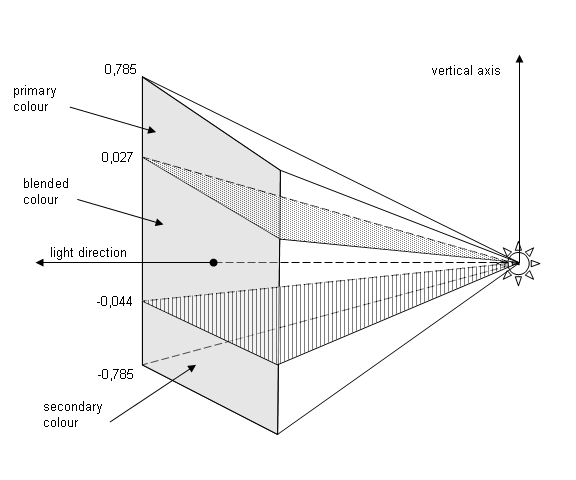
1. For an airplane approaching a runway, the colour of the approach lights can change depending on the relationship of the airplane to the correct approach slope as depicted in Figure 6.1.

   

   Figure 1 — <DRM Blend Directional Light> blend section example

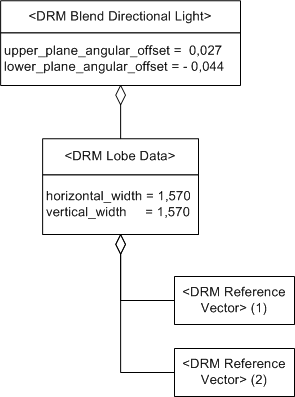
   This can be represented by a <Blend Directional Light> instance having both a primary and a secondary colour as depicted in Figure 6.2.

   

   Figure 2 — <DRM Blend Directional Light> example

   If the position of the observer is 0.177 radians (approximately 10 degrees) above the SE_REFVEC_LIGHT_DIRECTION vector of the <Lobe Data> instance, the observer will see the primary colour.

   If the position of the observer is 0.027 radians (approximately 1.5 degrees) above the SE_REFVEC_LIGHT_DIRECTION vector, the observer will see the primary colour, since the observer is at the upper edge of the blend section. As the observer moves lower, the amount of primary colour decreases as it is blended with proportionally increasing amounts of the secondary colour. Once the observer reaches -0.009 radians (approximately -0.5 degrees) from the SE_REFVEC_LIGHT_DIRECTION vector in the vertical direction (i.e., towards the negative end of the SE_REFVEC_VERTICAL_AXIS vector), the observer sees the primary and secondary colours blended in equal amounts as the observer is now in the middle of the blend section. As the observer continues to move in the same direction, the amount of primary colour continues to decrease proportionally as the amount of secondary colour increases. When the observer reaches -0.044 radians (approximately -2.5 degrees) from the SE_REFVEC_LIGHT_DIRECTION vector, the observer sees only the secondary colour, as he has now reached the lower edge of the blend section.

   If the position of the observer from the SE_REFVEC_LIGHT_DIRECTION vector is -0.177 radians (approximately -10 degrees) in the vertical direction (i.e., towards the negative end of the SE_REFVEC_VERTICAL_AXIS vector), the secondary colour is seen as the observer is inside the vertical width, in the lower section of the cone.

   If the position of the observer from the SE_REFVEC_LIGHT_DIRECTION vector is -0.884 radians (approximately -50 degrees) in the vertical direction (i.e., towards the negative end of the SE_REFVEC_VERTICAL_AXIS vector), nothing is seen as the observer is outside the pyramid.

FAQs

No FAQs supplied.

Constraints

• <<Publishable Object>>
• <<Inheritance Rule For Location>>

Composed of (two-way) (inherited)

• one <Lobe Data> instance¹
• one <Location> instance

Component of (two-way) (inherited)

• one or more <Light Rendering Properties> instances

Inherited Field Elements

Field Elements

Notes

Composed of Notes

Lobe_Data

Fields Notes

upper_plane_angular_offset

The upper_plane_angular_offset field specifies, in radians, the angular offset of the plane separating the upper and blend sections of the pyramid. The offset is measured from the given SE_REFVEC_LIGHT_DIRECTION vector of the <Lobe Data> instance along the SE_REFVEC_VERTICAL_AXIS vector of the <Lobe Data> instance.

lower_plane_angular_offset

The lower_plane_angular_offset field specifies, in radians, the angular offset of the plane separating the blend and lower sections of the pyramid. The offset is measured from the given SE_REFVEC_LIGHT_DIRECTION vector of the <Lobe Data> instance along the SE_REFVEC_VERTICAL_AXIS vector of the <Lobe Data> instance.

The upper_plane_angular_offset shall be greater than or equal to the lower_plane_angular_offset. Both planes shall be within the pyramid defined by the given <Lobe Data> instance.

The colour used to display the light is computed as follows.

Let:

U = upper_plane_angular_offset
L = lower_plane_angular_offset
O = observer angular offset
D = colour to display
P = primary colour
S = secondary colour

Then:

Case 1:  O ≥ U

D = P

Case 2:  L < O < U

D = ((O - L) × P + (U - O) × S) / (U - L)

Case 3:  O ≤ L

D = S